筱林同学的blog
0%

数据结构

发表于 更新于 分类于 热度： ℃ Valine：
数据结构转段复习知识点（部分）

引论

程序=数据结构+算法

数据结构的概念

数据：客观描述事物的数值、字符等及能被输入到计算机中且能被处理的各种符号集合。
数据元素：组成数据的基本单位，是数据集合的个体。一个元素由多个数据项组成，数据项是数据的最小单位。
数据对象：性质相同的数据元素的集合
数据结构：相互之间存在一种或多种特定关系的数据元素集合。
数据类型
数据抽象与抽象数据类型

数据结构的内容

数据结构的内容可归纳为三个部分：逻辑结构、存储结构、运算集合
数据的逻辑结构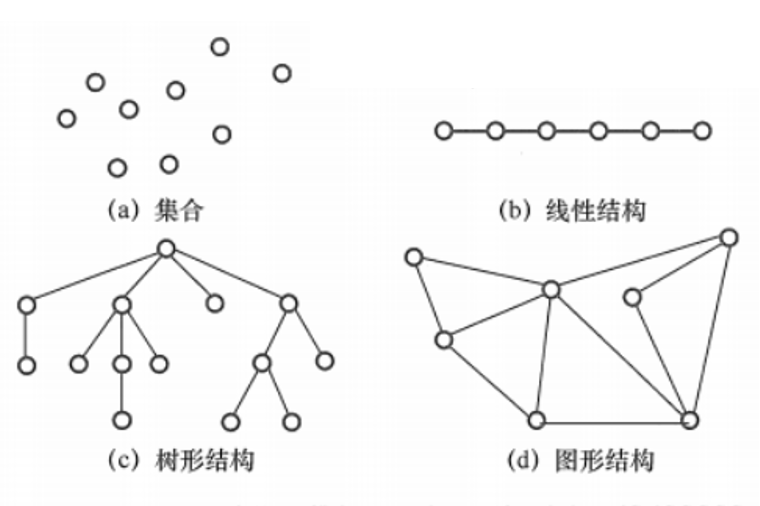
image-20211125205558173

数据的存储结构：顺序存储、链式存储

算法

算法：解决问题的一系列操作步骤的集合
算法的特性：

  • 有穷性：有限次的循环，不会产生死循环
  • 确定性：含义明确，不能有歧义
  • 可行性：算法的每一步必须是可行的
  • 有输入
  • 有输出

算法的评价标准：

  • 正确性
  • 可读性
  • 健壮性（鲁棒性）
  • 高效率与低存储

时间复杂度：算法基本操作（关键语句）重复执行的次数
空间复杂度：算法执行时所需存储空间的度量

线性表

线性表：元素之间具有“一对一”的前驱后继关系
基本操作：

1
2
3
4
5
6
InitList ( );                //初始化
lengthList ( );              //求表长
GetList (int i);             //取元素
InsertList (  i, x);         //插入
DeleteList(int i);           //删除
LocateList(  x);             //定位

顺序存储

顺序存储（数组）：连续的按排列顺序存储表中元素

定义

1
2
3
4
5
6
7
#define  MAXSIZE  100                // 假设最大容量
  typedef  int  ElemType;         // 假设元素类型为int, 具体根据实际情况确定
   
   typedef  struct {
           ElemType   elem[MAXSIZE];       //数组
           int  length ;               //元素实际个数
   } SeqList;

插入

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void   InsertList ( Sqlist &L,  int  i,   ElemType  e )
{                     
     if (L.length==MAXSIZE)       
                     printf( “表满” );   
     else  if ( i<1||i>L.length+1 )      
                    printf( “位置错” ); 
     else {                       
               for( j=L.length-1 ;  j>=i-1 ;  j-- )   //移动元素，腾空间
                        L.elem[ j+1]=L.elem[ j];  

                L.elem[i-1]=e;    //插入 
                L.length++;      //表长加1
        }
}

删除

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void  DeleteList( SqList &L,  int i  ) /*   删除第i个元素   */
{
        if ( L.length==0 )      
               printf(“表空”);
        else    if ( i<1) || (i>L.length )     
                            printf(“i值不合理”);
                   else      
                          {          //数据向前移动 , 覆盖第i个元素 
                                 for ( j=i ;  j < L.length ;  j++ )
                                          L.elem[ j-1] = L.elem[ j ]; 

                                  L.length--;     //表长减1
                          }
}

查找

1
2
3
4
5
6
7
8
9
10
11
 
int   Locate ( SqList L  , ElemType  x )
 {
         for (int  i=0; i<L.length ; i++ )    //遍历 

                if  ( e == L.data[i] )  
                        return  i+1 ;      //找到，返回位置

         return   0 ;     //没有找到
}

链式存储

链式存储：每个元素存有后继元素的地址

  • 结点在内存的位置任意，不一定连续。
  • 用“指针”（地址）将它们链连起来。
    每个”结点”含有两部分：元素值、指针

定义

1
2
3
4
5
//     结点      
typedef  struct  Node  {
      ElemType        data;    //数据 
      struct   Node     *next;   //指针    
  } LNode,  *LinkList;

单链表

创建单链表（头插）
  1. 建立头结点
    1
    2
    L=(LinkList) malloc (sizeof(LNode));
    L->next=NULL;
  2. 建立新结点
    1
    p=(LinkList) malloc (sizeof(LNode));
  3. 插入在头部
    1
    2
    p->next=L->next;
    L->next=p;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

LinkList   Creat ( int  n)        /*     建立长度为n的单链表( 头插法)     */
{
   LinkList   L=(LinkList) malloc (sizeof(LNode));      //建立头结点
   L->next=NULL  ;                   //初始也是尾结点
    for  (int  i=1; i<=n;  i++)     
    {
                s=(LinkList)malloc(sizeof(LNode));               //新结点
         scanf(“%d”, s->data);                        //输入数据元素                  
                p->next=L->next;               //插入在表头
         L->next=p;
     }

return   L ;        //返回头指针
}
创建结点

当建立新结点时，需要申请一个结点空间。如：

1
p=(ListNode*)malloc(sizeof(ListNode))

将该空间的首地址存入指针变量P中。

释放结点

动态分配的存储空间在用完后一定要释放。否则，造成内存泄露。如：
free(p)
释放由p指向的内存区（结点）。

按序号查找
1
2
3
4
5
6
7
8
9
10
11
12
13
LinkList   Get_LinkList(LinkList H，int k )  
{
        int  j=1;                  
        LinkList  p=H ;    //从头开始
        while( p->next && j<k)   {
                 p=p->next;       //p移动到下一个结点
                 j++;
         }
          if(j==k)   
                 return   p ;   //找到第k个元素，返回指针
           else   
                 return  null;  
}
删除

修改 p 的后继地址：
p->next = p->next->next

1
2
3
4
5
6
7
8
9
10
11
12
13
int   Del_LinkList(  LinkList  &H ,  int i  ) 
{ 
	LinkList   q  ,  p;
	p=Get_LinkList(H,i-1);    //寻找第i-1个元素  
	if ( p->next==NULL ) 
	           printf(“第i个元素不存在 “);
	else  {
                             q = p->next;               // q是p的后继，即第i个结点   
	             p->next = q->next;	 //修改链，删除q 
	             e = q->data;                
	             free(q);                    //释放q  
	} 
}
插入

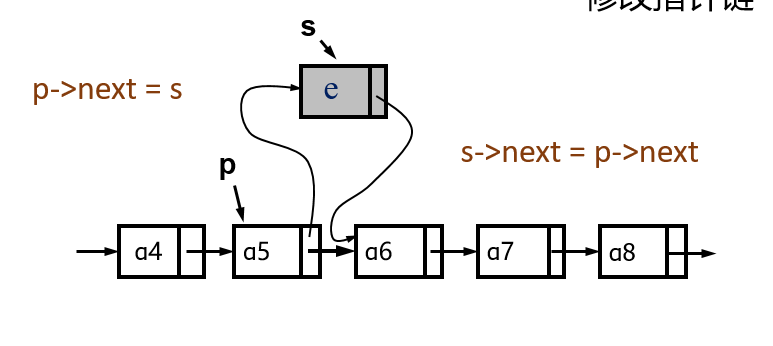
image-20211125182237140

1
2
3
4
5
6
7
8
9
10
11
12
13
int  Insert_LinkList( LinkList &L,  int  i  ,   ElemType  x )      
{   
	LinkList  s , p;
	p=Get_LinkList(H,i-1);   /* 寻找i的前驱结点，让p指向它 */
	if (p==NULL || j > i-1) 
		printf(“第i个元素不存在 “);
	else  {
		s = (LinkList)malloc(sizeof(Node));     /*  创建新结点 */
		s->data = e;  
		s->next = p->next;       /* 修改链，插入在p之后  */
		p->next = s;   
	}        
}

循环链表

尾结点的后继是头结点

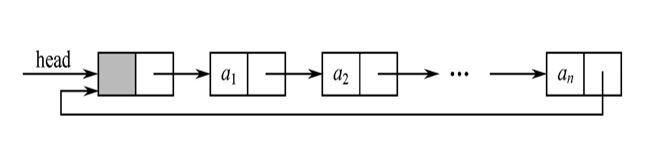
image-20211125195853719

从任一结点出发可以到达其它结点

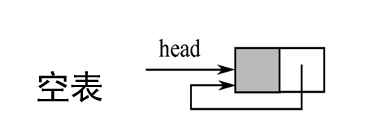
image-20211125195925107

双向链表

每个结点有两个指针，分别指向其前驱和后继。

优点： 双向遍历

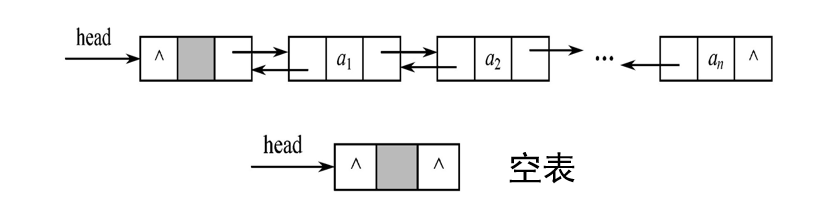
image-20211125200011789

插入

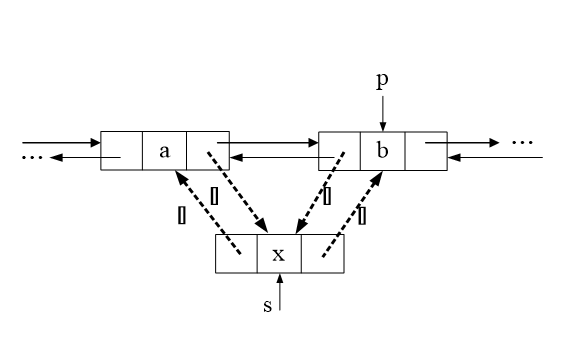
image-20211125200048655

修改4个指针

1
2
3
4
① s.prior=p.prior;  
② p.prior.next=s;
③ s.next=p;        
④ p.prior=s;
删除

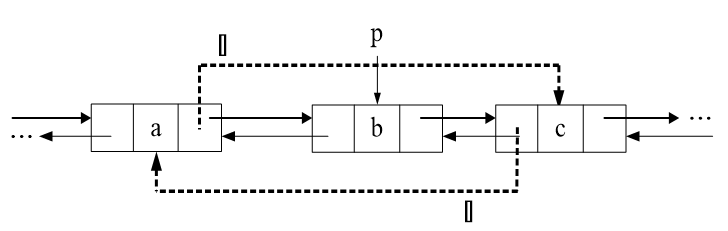
image-20211125200149823

修改2个指针

① p.prior.next=p.next;
② p.next.prior =p.prior;

顺序表和链表的比较

顺序表：

  1. 存储紧凑；

  2. 可以快速地存取表中任一位置的元素；

  3. 插入删除元素需要移动大量元素；

  4. 表的容量难以确定和扩充。

链表：

  1. 插入删除仅需修改指针；

  2. 表的长度可以动态变化；

  3. 存取某元素需要从头遍历表；

  4. 每个元素需要附加一个指针域。

栈和队列

栈

栈(Stack)是限制在表的一端进行插入和删除运算的线性表，插入、删除的一端为栈顶(Top)，另一端为栈底(Bottom)。top== -1时为空栈，top==0只能说明栈中只有一个元素，元素进栈时top自增
特性：先进后出
存储结构：顺序存储、链式存储
顺序存储栈（数组）：顺序存储结构
链栈：链式存储结构。插入和删除仅在链头操作。栈顶指针是链表的头指针。不需要判断栈满，只需要判断栈空。
栈空：top == -1
栈满： top = max-1
**双栈共用共享：栈1的底在V[1]，栈2的底在V[m]，栈满条件： **top[1]+1=top[2]。

n个元素入栈，可能的出栈序列有C(2n,n)/(n+1)个。（C(2n，n)，求2n前n位的阶乘）

双栈共享

一个数组用于两个栈

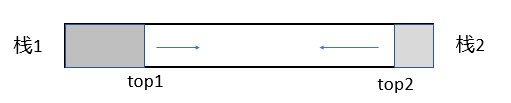
image-20211125203249109

栈满： top1+1==top2

栈1空：top1==-1

栈2空：top2==M (M为顺序表容量）

入栈1：top1++

入栈2: top2–

队列

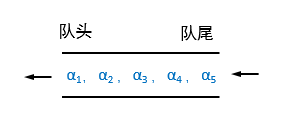
image-20211125201635557

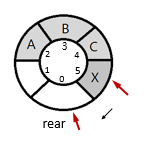
队列(Queue)也是一种运算受限的线性表。插入和删除分别在两端，意味着它只允许在表的一端进行插入，而在另一端进行删除。允许删除的一端称为队头(front)，允许插入的一端称为队尾(rear)。
特性：先进先出。
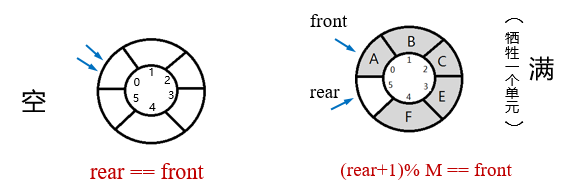
队空条件：rear == front
队满条件：（rear+1）% MAX = = front （MAX=队列的最大长度）
计算队列长度：（rear-front+QueueSize）% QueueSize
入队：（rear+1）% QueueSize = rear
出队：（front+1）% QueueSize = front

链式队列

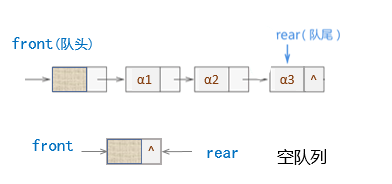
image-20211125201744158

定义链队列：

1
2
3
4
5
typedef   struct 
{
       LNode  * front;
       LNode  *rear;
} LinkQueue;

链式存储结构。限制仅在表头删除和表尾插入的单链表。显然仅有单链表的头指针不便于在表尾做插入操作，为此再增加一个尾指针，指向链表的最后一个结点。

出队

删除队首

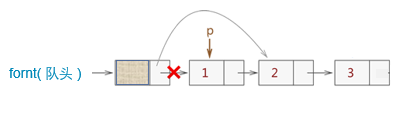
image-20211125201901938

修改指针：Q. front -> next = p->next;

释放结点：free(p)

入队

插入队尾

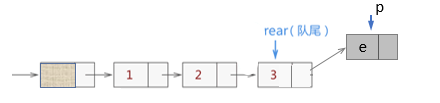
image-20211125202031693

插入队尾： Q.rear->next = p;

新队尾 ： Q.rear = p ;

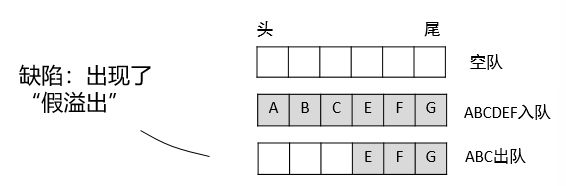
顺序队列

顺序存储结构。当头尾指针相等时队列为空。在非空队列里，头指针始终指向队头前一个位置，而尾指针始终指向队尾元素的实际位置。

image-20211125202133611

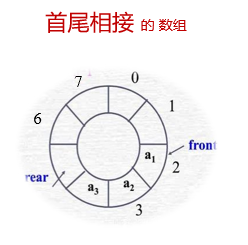
循环队列

循环队列。在循环队列中进行出队、入队操作时，头尾指针仍要加1，朝前移动。只不过当头尾指针指向向量上界（MaxSize-1）时，其加1操作的结果是指向向量的下界0。除非向量空间真的被队列元素全部占用，否则不会上溢。因此，除一些简单的应用外，真正实用的顺序队列是循环队列。故队空和队满时头尾指针均相等。因此，我们无法通过front=rear来判断队列“空”还是“满”。

image-20211125202244592

**队头指针移动一个位置:**front = (front+1) % Size

队尾指针移动一个位置: rear = (rear+1) % size

image-20211125202845060

出队

image-20211125202931015

1
2
3
4
5
6
7
8
9
10
int  DeQueue(SqQueue &Q , DataType &x) 
{
	if( Q.front==Q.rear )  
		   printf("队列空!");
	else 
         {	
	          x=Q.base[Q.front];        // 删除 
	          Q.front=(Q.front+1)%M;  //新的队头  
	   }
}

image-20211125203030591

1
2
3
4
5
6
7
8
9
10
void  EnQueue(SqQueue &Q , ElemType  x) 
{
	if( (Q.rear+1)%M==Q.front )  
		printf("队列满!");
	 else  
         {
	           Q.base[Q.rear] = x;       // 插入 
	           Q.rear=(Q.rear+1)%M;   // 新的队尾  
	  }
}

树和二叉树

树的定义和基本术语

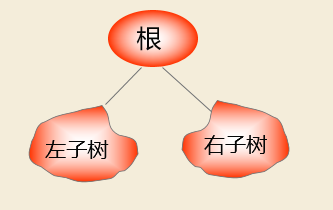
树的定义

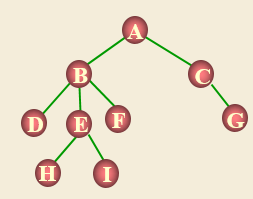
image-20211201192649382

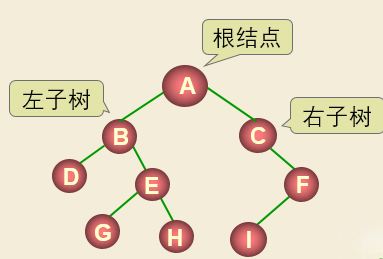
  • 一个“根”：A

  • 一些“子树”：T1={B,D,E,F,H,I} , T2={C,G}

  • 每个子树还有自己的根和子树

  • 树是非线性结构

  • 元素是“一对多”关系

  • 树是层次结构

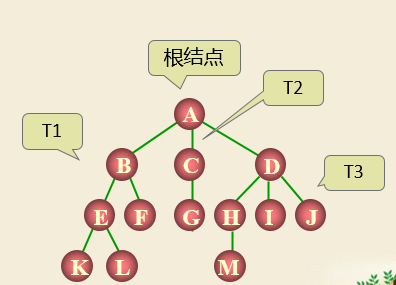
image-20211201192944437

树的各种表示：

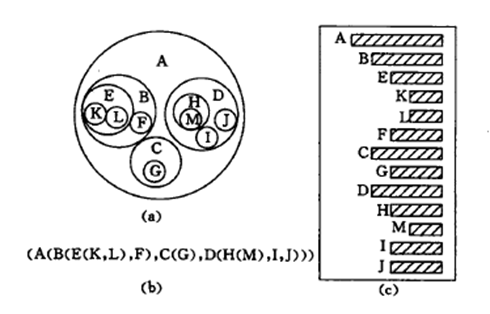
image-20211201193151162

树的基本术语

  • 结点
  • 结点的度
  • 叶子结点
  • 分支结点
  • 孩子结点
  • 父亲结点
  • 兄弟结点
  • 祖先结点
  • 树的度
  • 结点的层次
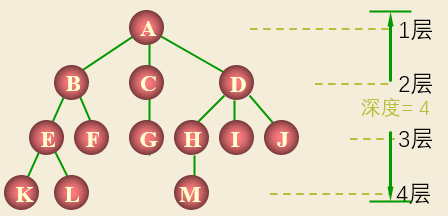
  • 树的深度
  • 森林

image-20211201193519967

二叉树的性质与存储

二叉树： 每个结点最多有2个子树，有左右子树之分 。

image-20211201193757387

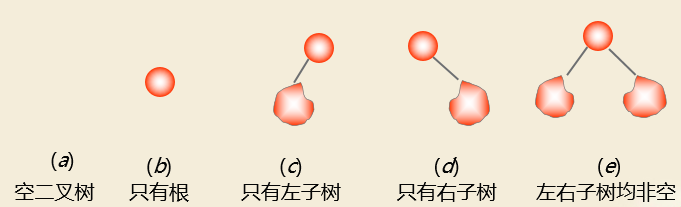
二叉树的5种基本形态：

image-20211201194331751

满二叉树：所有分支结点都有2棵子树；所有叶子结点都在同一层上。

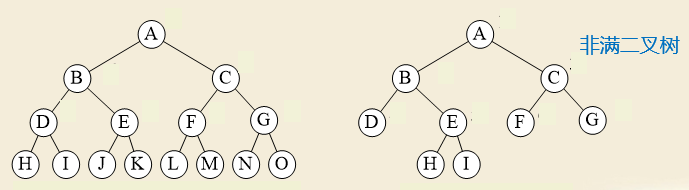
image-20211201194446257

完全二叉树：完全二叉树 上面的层都是满的，最后一层可以缺右边的连续个叶子

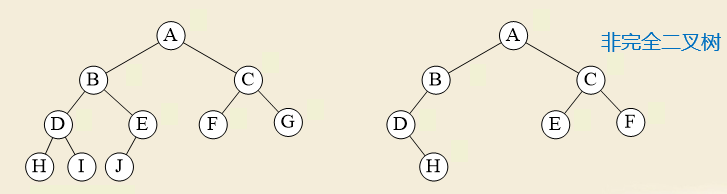
image-20211201194525417

二叉树的性质

性质1 ：一棵非空的二叉树的第 i 层上至多有 2i －1个结点(i ³ 1)。

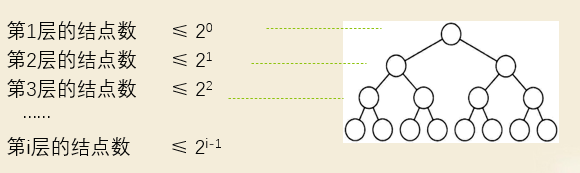
image-20211201194646997

性质2：一棵深度为k的二叉树中，最多具有2k－1个结点。

总的结点数＝第1层+第2层+第3层+ …+ 第k层

    ≤  20 +  21 + 22  +… + 2k-1   = 2k -1

性质3：对于一棵非空的二叉树，如果叶子结点数为n0，度数为2的结点数为n2，则有: n0＝n2＋1。

总的结点数： n=n0+n1+n2 ①
总的分支数： B=n1+2n2 ②
总的分支数： B=n-1 ③
由①②③ 得 ： n0=n2+1

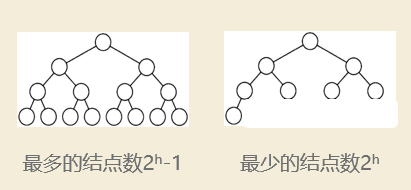
性质4： 具有n个结点的完全二叉树的深度为 ⌊ log2n ⌋+1。
2h-1 ≤ n ≤ 2h-1
2h-1 ≤ n ＜ 2h
h-1 ≤ log2n ＜ h
h = [log2n]＋1

image-20211201194947312

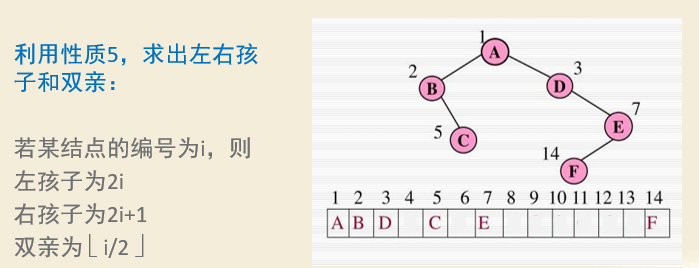
性质5：对于完全二叉树，对结点从左到右按层从1开始编号，则对于序号为i的结点，有：
（1）如果i＝1，则该结点是根结点；
（2）序号为i的结点的左子结点的序号为2i；
（3）序号为i的结点的右子结点的序号为2i＋1；
(4) 序号为i的结点的父结点的序号为 ⌊i/2⌋。

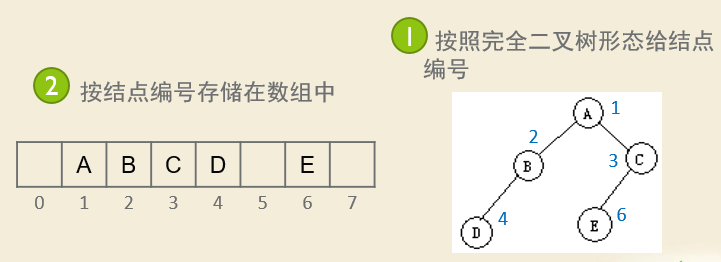
image-20211201195128014

image-20211201195152422

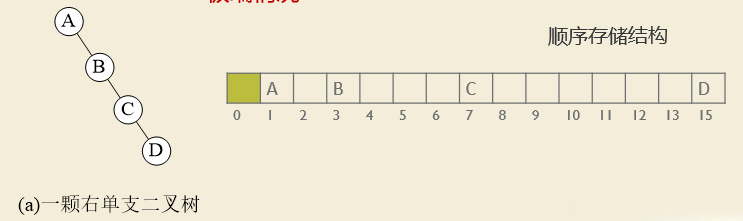
极端情况：

image-20211201195245224

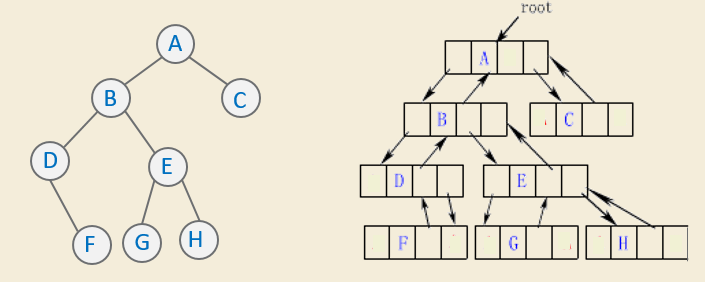
链式存储结构

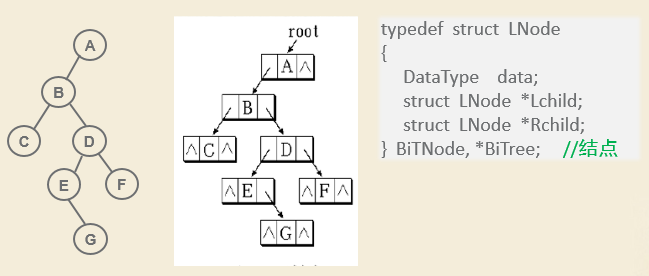
image-20211201195408608

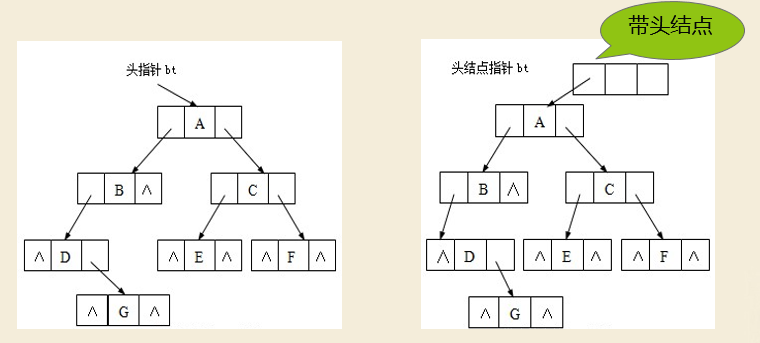
二叉链表的两种表示：

image-20211201195613903

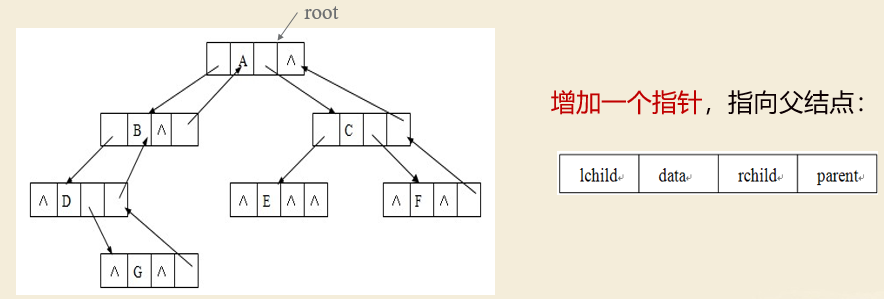
三叉链表：添加一个指针，指向双亲

image-20211201195651741

image-20211201195902273

二叉树遍历

访问二叉树中的每个结点，使每个结点仅被访问一次。

依次遍历二叉树中的三个组成部分

image-20211201195945963

先序遍历

先序遍历（DLR）
若非空，则：
(1) 访问根结点；
(2) 先序遍历左子树；
(3) 先序遍历右子树。

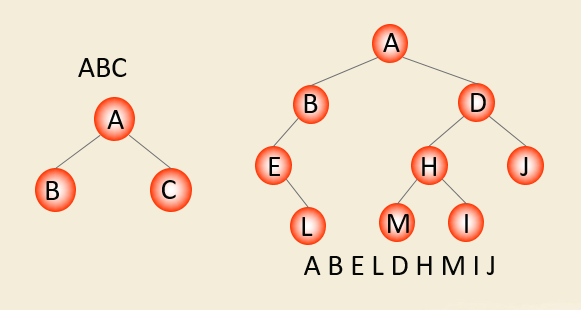
image-20211201200106422

注意：子树也是一棵树，也要按照先序遍历

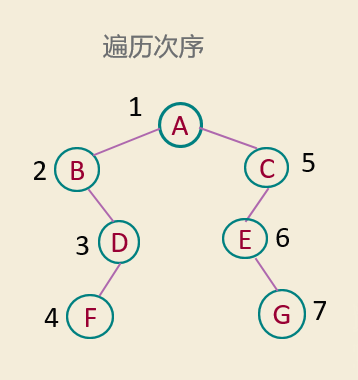
image-20211201200237413

中序遍历

中序遍历（DLR）
若二叉树非空，则
(1) 中序遍历左子树；
(2) 访问根 ；
(3) 中序遍历右子树。

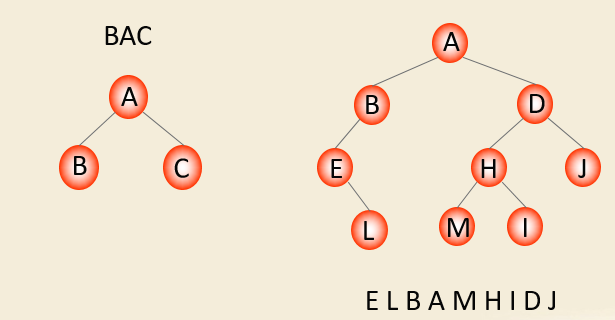
image-20211201200429967

后序遍历

若二叉树非空，则：
(1) 后序遍历左子树；
(2) 后序遍历右子树；
(3) 访问根 。

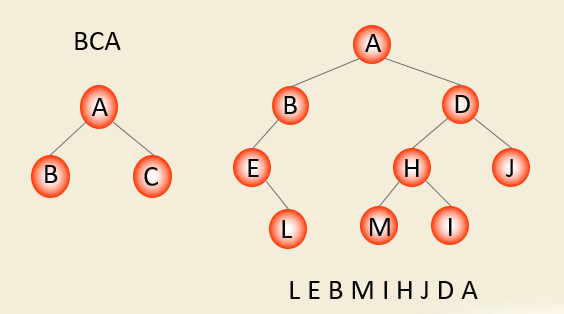
image-20211201200703220

遍历二叉树归纳：

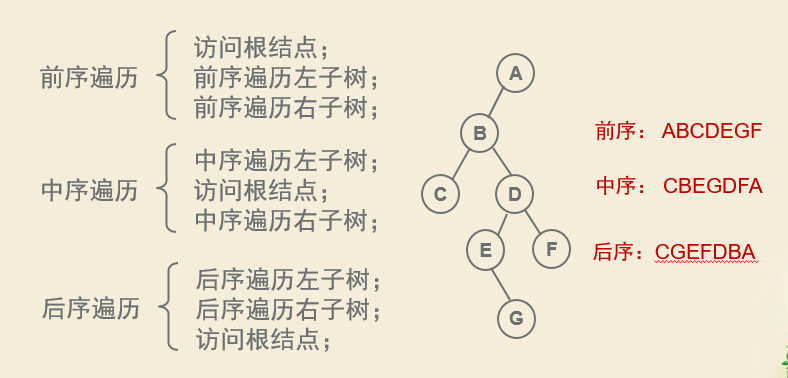
image-20211201200639947

image-20211201201112368

遍历二叉树递归程序

先序遍历：

1
2
3
4
5
6
7
void  preOrder( BiTree  root )  {   
         if  (root!=NULL)  {
                   visite( root );       //访问根
                   preOrder(root.lchild);    //遍历左子树
                   preOrder(root.rchild);  //遍历右子树
         }
 }

中序遍历：

1
2
3
4
5
6
7
8
void  inOrder( BiTree  root )  {   
         if  (root!=NULL)  {
	inOrder(root.lchild);    //遍历左子树
                    visite( root );      //访问根
	inOrder(root.rchild);  //遍历右子树
         }
 }

后续遍历：

1
2
3
4
5
6
7
8
void  postOrder( BiTree  root )  {   
         if  (root!=NULL)  {
	postOrder(root.lchild);    //遍历左子树
                postOrder(root.rchild);  //遍历右子树
       	visite( root);      //访问根
  }
 }

二叉树的应用

查找

顺序查找

查找表的结构

查找表的结构，决定了查找数据的方式

  • 查找表是一组无序的数据；
  • 查找表是一组有序的数据；
  • 查找表是线性结构；
  • 查找表是非线性结构。

查找分类

静态查找表
只查找，不改变表的数据

动态查找表
在查找过程中，修改表中的数据（插入、删除）

平均查找长度（平均比较次数）

image-20211202160554475

顺序查找

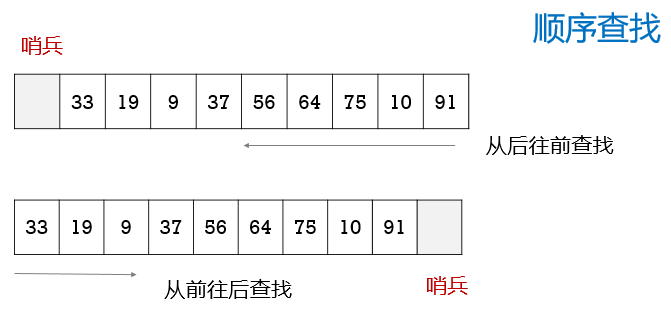
image-20211202160712072

1
2
3
4
5
6
7
8
9
10
11
int  linerSearch ( SeqRList  L ,    keyType  k )   {

        L.r[ 0 ] .key = k;      //监视哨
        i=L.length;

        while( L.r[ i ] .key != k)    //反向查找
                  i--;  
 
        return     i;     //返回位置，失败时i=0
}

优点：算法简单，适应面广

缺点：平均查找长度大，

顺序查找的性能

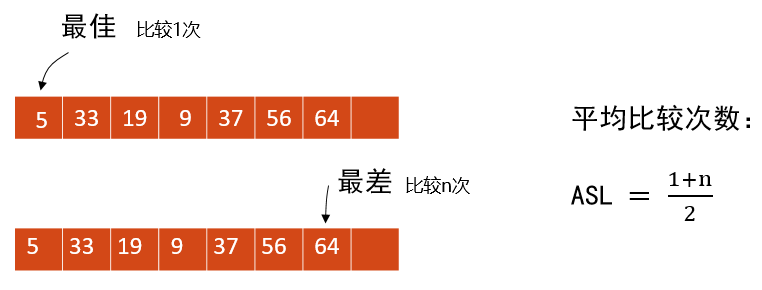
image-20211202160745279

image-20211202160833368

折半查找

image-20211202185151523

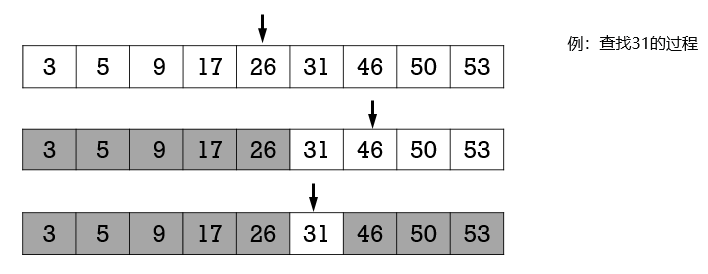
image-20211202185241561

折半查找性能

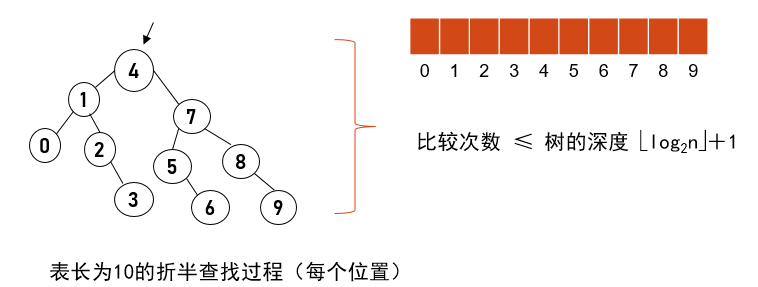
image-20211202185315320

折半查找实现

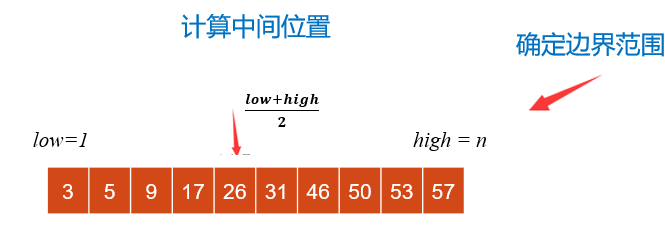
image-20211202185346353

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int   binarySearch( SSTable  ST,  int  key )   {

	     int    low = 1 ， high = ST.length;      // 初始上界、下界

	     while ( low <= high )   {
		    int   mid = ( low+high )/2;     // 中间位置
		    if ( key == ST.elem[mid] )
			     return    mid;           //成功，返回位置
		    else  if ( key < a[mid] )
			      high = mid-1;         //左半边继续查找
		    else
			      low = mid+1;      //右半边继续查找
	     }
	     return    0;     // 失败
}

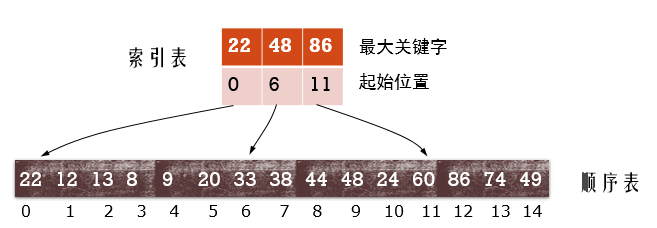
索引表查找

image-20211202185455002

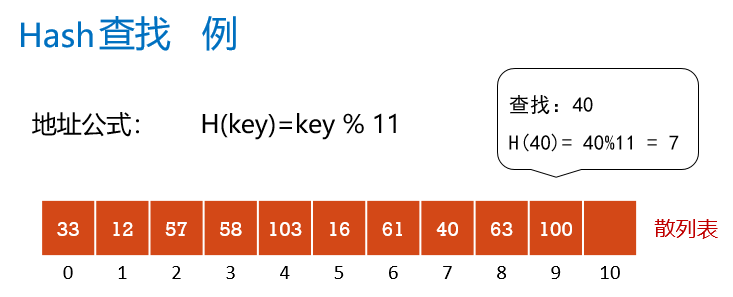
哈希查找

哈希表查找（散列）

查找时不需要进行比较；
直接通过公式直接计算出元素的地址（位置）。

image-20211202185609904

image-20211202185659001

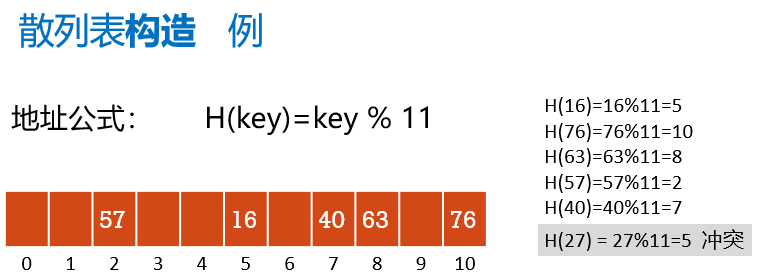
image-20211202185709009

哈希函数的构造方法

直接地址法

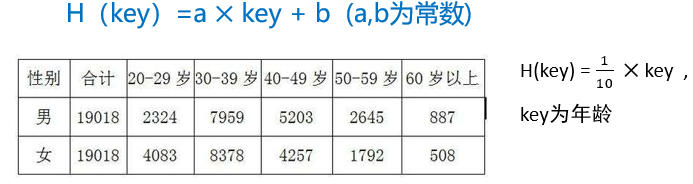
image-20211202185808890

除留取余法

image-20211202185833888

平方取中法

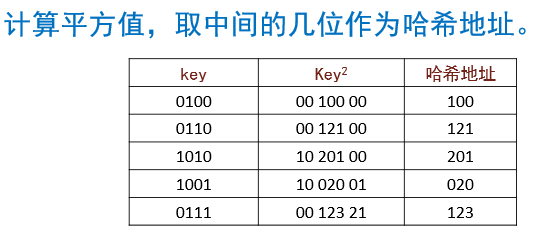
image-20211202185853290

数字分析法

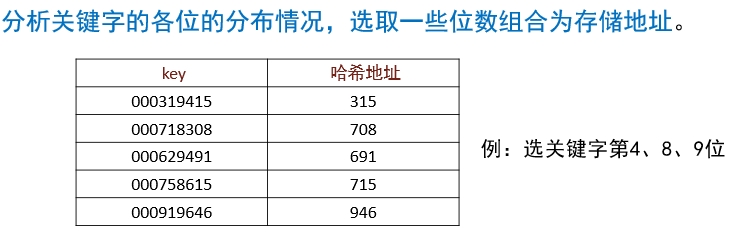
image-20211202185909642

处理冲突的方法

开放定址法之“线性探测法 ”

若在地址t处冲突，则从t开始顺次探测相邻的下一个空闲位置

image-20211202190015633

例：

image-20211202190119763

image-20211202190146220

链地址法

相同地址的关键字，同一个链表中

image-20211202190235561

如果觉得对你有用的话，不妨支持一下